Kumpulan soal latihan trigonometri mulai dari konsep dasar hingga soal analisis (HOTS) dan TKA.
A. Kategori Low/Middle (Konsep Dasar)—10 Soal
1. Menentukan Tinggi Dinding
Sebuah tangga sepanjang 10 m disandarkan pada dinding dan membentuk sudut \(60^\circ\) dengan lantai. Tinggi dinding yang dicapai tangga adalah...
Penyelesaian:
Diketahui sisi miring = 10 m dan sudut \(60^\circ\).
$$\sin 60^\circ = \frac{t}{10}$$ $$\frac{\sqrt{3}}{2} = \frac{t}{10}$$ $$t = 5\sqrt{3} \text{ m}$$2. Sudut Depresi Mercusuar
Dari puncak mercusuar setinggi 40 m, pengamat melihat kapal A (sudut depresi \(30^\circ\)) dan kapal B (sudut depresi \(45^\circ\)) segaris lurus. Jarak antara kapal A dan B adalah...
Penyelesaian:
Jarak A \(= \frac{40}{\tan 30^\circ} = 40\sqrt{3}\)
Jarak B \(= \frac{40}{\tan 45^\circ} = 40\)
Jarak AB \(= 40\sqrt{3} - 40 = 40(\sqrt{3}-1) \text{ m}\)
3. Menentukan Nilai Tan
Jika \(\sin \theta = \frac{2}{3}\) dan \(\theta\) di kuadran I, maka \(\tan \theta\) adalah….
Penyelesaian:
Sisi samping \(= \sqrt{3^2 - 2^2} = \sqrt{5}\)
$$\tan \theta = \frac{De}{Sa} = \frac{2}{\sqrt{5}} = \frac{2}{5}\sqrt{5}$$4. Nilai Sudut Istimewa
Nilai \(\sin 30^\circ, \cos 45^\circ, \tan 60^\circ, \sin 90^\circ\) secara berurutan adalah….
Penyelesaian:
\(\frac{1}{2}, \frac{1}{2}\sqrt{2}, \sqrt{3}, 1\)
5. Menentukan Cosecan
Diketahui \(\tan \theta = \frac{5}{4}\), nilai \(\text{cosec } \theta = \dots\)
Penyelesaian:
Sisi Miring \(= \sqrt{5^2 + 4^2} = \sqrt{41}\)
$$\text{cosec } \theta = \frac{Mi}{De} = \frac{\sqrt{41}}{5}$$6. Perbandingan Sisi Segitiga
Diketahui segitiga ABC siku-siku di B. Jika nilai \(\sin A = \frac{5}{13}\), maka nilai dari \(\tan C\) adalah...
Penyelesaian:

Diketahui \(\sin A = \frac{5}{13} = \frac{De}{Mi}\).
Cari sisi \(Sa\) (Samping AB): \(\sqrt{13^2 - 5^2} = \sqrt{144} = 12\).
Untuk sudut C, sisi Depan adalah AB (12) dan Samping adalah BC (5).
$$\tan C = \frac{De}{Sa} = \frac{AB}{BC} = \frac{12}{5}$$7. Identitas Penjumlahan Sudut
Nilai dari \(\sin 30^\circ \cdot \cos 60^\circ + \cos 30^\circ \cdot \sin 60^\circ\) adalah....
Penyelesaian:
$$= \left(\frac{1}{2} \cdot \frac{1}{2}\right) + \left(\frac{1}{2}\sqrt{3} \cdot \frac{1}{2}\sqrt{3}\right)$$ $$= \frac{1}{4} + \frac{3}{4} = \frac{4}{4} = 1$$8. Operasi Kuadrat Trigonometri
Nilai dari ekspresi \(\frac{\sin^2(45^\circ) \cdot \cos^2(30^\circ)}{\tan(60^\circ)}\) adalah...
Penyelesaian:
Pembilang: \((\frac{\sqrt{2}}{2})^2 \cdot (\frac{\sqrt{3}}{2})^2 = \frac{2}{4} \cdot \frac{3}{4} = \frac{3}{8}\)
Penyebut: \(\sqrt{3}\)
$$= \frac{3}{8\sqrt{3}} = \frac{3\sqrt{3}}{24} = \frac{1}{8}\sqrt{3}$$9. Menentukan Nilai Cosinus
Diketahui segitiga PQR siku-siku di Q. Jika panjang sisi \(PQ = 12\) dan \(QR = 5\), maka nilai \(\cos P\) adalah...
Penyelesaian:
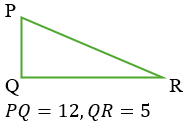
Sisi Miring \(PR = \sqrt{12^2+5^2} = \sqrt{169} = 13\).
$$\cos P = \frac{Sa}{Mi} = \frac{PQ}{PR} = \frac{12}{13}$$10. Operasi Campuran Sudut Istimewa
Nilai dari \((\sin 30^\circ + \cos 0^\circ) \cdot \sin 45^\circ\) adalah...
Penyelesaian:
$$= \left(\frac{1}{2} + 1\right) \times \frac{1}{2}\sqrt{2}$$ $$= \frac{3}{2} \times \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{4}$$B. Kategori Middle/High (HOTS: Analisis dan Penalaran Kuantitatif)—3 Soal
1. Cosinus Sudut Tangga
Sebuah tangga sepanjang 5 meter disandarkan pada sebuah dinding. Jarak ujung bawah tangga ke dinding adalah 3 meter. Berapakah nilai cosinus dari sudut yang dibentuk oleh tangga dan lantai?
Penyelesaian:
Diketahui Sa = 3 m, Mi = 5 m.
$$\cos \theta = \frac{Sa}{Mi} = \frac{3}{5}$$2. Mengukur Tinggi Pohon (Klinometer)
Andi berdiri 12 meter dari sebatang pohon dengan sudut elevasi \(30^\circ\). Jika tinggi Andi 1,5 meter, berapakah tinggi total pohon?
Penyelesaian:
Cari tinggi pohon dari mata ke atas (\(x\)):
$$x = 12 \times \tan 30^\circ = 12 \times \frac{1}{\sqrt{3}} = 4\sqrt{3} \text{ m}$$Total = \(4\sqrt{3} + 1,5 \approx 8,42 \text{ m}\).
3. Operasi Campuran Trigonometri
Hasil dari \(\frac{\sin 270^\circ \cdot \cos 135^\circ \cdot \tan 135^\circ}{\sin 150^\circ \cdot \cos 225^\circ} = \dots\)
Penyelesaian:
Substitusi nilai:
$$= \frac{(-1) \times (-\frac{1}{2}\sqrt{2}) \times (-1)}{(\frac{1}{2}) \times (-\frac{1}{2}\sqrt{2})}$$Sederhanakan dengan mencoret \(-\frac{1}{2}\sqrt{2}\):
$$= \frac{(-1) \times (-1)}{\frac{1}{2}} = \frac{1}{\frac{1}{2}} = 2$$C. Mini TKA—5 Soal
1. Jarak Pelampung ke Jembatan
Dari atas jembatan, sudut depresi pelampung adalah \(30^\circ\). Jika tinggi jembatan 65 meter, jarak pelampung ke tepi jembatan adalah...
Penyelesaian:
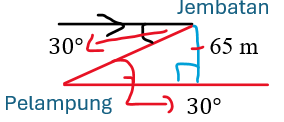 $$\sin 30^\circ = \frac{65}{x}$$
$$\frac{1}{2} = \frac{65}{x} \rightarrow x = 65 \times 2 = 130 \text{ m}$$
$$\sin 30^\circ = \frac{65}{x}$$
$$\frac{1}{2} = \frac{65}{x} \rightarrow x = 65 \times 2 = 130 \text{ m}$$
2. Segitiga Sembarang
Sebuah \(\Delta PQR\) dengan \(\Delta PQR = 45^\circ\), \(\angle SPR = 30^\circ\), dan \(QR = 6\) cm. Tentukan \(PQ\) dan \(PR\)!
Penyelesaian:
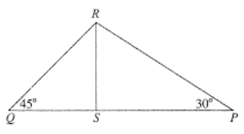
1. Mencari RS:
$$\sin 45^\circ = \frac{RS}{6} \rightarrow \frac{1}{2}\sqrt{2} = \frac{RS}{6}$$ $$RS = 3 \text{ cm (Sesuai kunci: 3 cm)}$$2. Cari QS:
$$\tan 45^\circ = \frac{3}{QS} \rightarrow 1 = \frac{3}{QS} \rightarrow QS = 3 \text{ cm}$$3. Cari RP:
$$\sin 30^\circ = \frac{3}{RP} \rightarrow \frac{1}{2} = \frac{3}{RP} \rightarrow RP = 6 \text{ cm}$$4. Cari SP:
$$\tan 30^\circ = \frac{3}{SP} \rightarrow \frac{1}{\sqrt{3}} = \frac{3}{SP} \rightarrow SP = 3\sqrt{3} \text{ cm}$$Jadi:
\(PQ = QS + SP = 3 + 3\sqrt{3} = 3(1+\sqrt{3})\) cm dan \(RP = 6\) cm.
3. Aturan Sinus
Diketahui \(\Delta ABC\) dengan besar \(\angle A = 60^\circ, \angle B = 45^\circ\), dan Panjang sisi \(BC = 8\) cm. Panjang sisi \(AC\) adalah....
Penyelesaian:
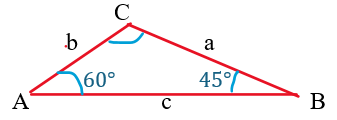 $$\frac{a}{\sin A} = \frac{b}{\sin B} \rightarrow \frac{8}{\sin 60^\circ} = \frac{AC}{\sin 45^\circ}$$
$$\frac{8}{\frac{\sqrt{3}}{2}} = \frac{AC}{\frac{\sqrt{2}}{2}}$$
$$AC = \frac{8 \times \frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} = \frac{8\sqrt{2}}{\sqrt{3}}$$
$$AC = \frac{8\sqrt{6}}{3}$$
$$\frac{a}{\sin A} = \frac{b}{\sin B} \rightarrow \frac{8}{\sin 60^\circ} = \frac{AC}{\sin 45^\circ}$$
$$\frac{8}{\frac{\sqrt{3}}{2}} = \frac{AC}{\frac{\sqrt{2}}{2}}$$
$$AC = \frac{8 \times \frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} = \frac{8\sqrt{2}}{\sqrt{3}}$$
$$AC = \frac{8\sqrt{6}}{3}$$
4. Menentukan Kosinus Sudut
Sebuah segitiga ABC dengan Panjang \(AB = 6\) cm, \(BC = 5\) cm, dan \(AC = 4\) cm. Nilai kosinus sudut B adalah....
Penyelesaian:
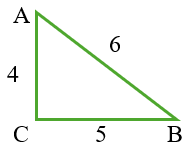
Berdasarkan gambar, diasumsikan siku-siku di C:
$$\cos B = \frac{Sa}{Mi} = \frac{5}{6} \text{ cm}$$5. Identitas Trigonometri
Bentuk sederhana dari \(\frac{\sin x \cdot \cos x}{\tan x}\) adalah....
Penyelesaian:
$$\frac{\sin x \cdot \cos x}{\tan x} = \frac{\sin x \cdot \cos x}{\frac{\sin x}{\cos x}}$$ $$= \sin x \cdot \cos x \cdot \frac{\cos x}{\sin x}$$ $$= \cos^2 x$$