Kumpulan soal latihan Geometri dan Pengukuran mulai dari konsep dasar sudut, bangun ruang sisi datar, hingga bangun ruang sisi lengkung.
A. Kategori Low/Middle (Konsep Dasar)—5 Soal
1. Pasangan Sudut Berseberangan
Diketahui \(\angle A\) dan \(\angle B\) merupakan pasangan sudut dalam berseberangan. Jika \(\angle A = (3x + 10)^\circ\) dan \(\angle B = (x + 42)^\circ\), maka nilai \(x\) adalah....
Penyelesaian:
Sudut dalam berseberangan memiliki besar yang sama:
$$\angle A = \angle B$$ $$3x + 10 = x + 42$$ $$2x = 32$$ $$x = 16$$2. Sudut pada Garis Sejajar
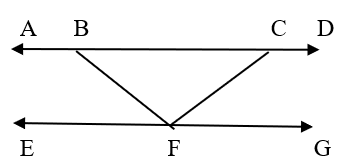
Perhatikan gambar di atas. Jika \(\angle EFB = 65^\circ\) dan \(\angle FCD = 120^\circ\), maka besar \(\angle BCF\) adalah....
Penyelesaian:
Pasangan sudut berpelurus (jumlah \(180^\circ\)):
$$\angle BCF + \angle FCD = 180^\circ$$ $$\angle BCF + 120^\circ = 180^\circ$$ $$\angle BCF = 60^\circ$$3. Luas Bahan Prisma Belah Ketupat
Vina membuat kotak pensil berbentuk prisma belah ketupat tanpa tutup. Diketahui keliling alas \(80 \text{ cm}\) dan panjang salah satu diagonalnya \(32 \text{ cm}\). Tinggi kotak \(30 \text{ cm}\). Luas bahan yang digunakan adalah...
Penyelesaian:
1. Sisi alas (\(s\)): \(K = 4s \rightarrow 80 = 4s \rightarrow s = 20 \text{ cm}\).
2. Cari diagonal kedua (\(d_2\)) dengan Pythagoras:
$$(\frac{d_1}{2})^2 + (\frac{d_2}{2})^2 = s^2$$ $$16^2 + (\frac{d_2}{2})^2 = 20^2 \rightarrow 256 + (\frac{d_2}{2})^2 = 400$$ $$(\frac{d_2}{2})^2 = 144 \rightarrow \frac{d_2}{2} = 12 \rightarrow d_2 = 24 \text{ cm}$$3. Luas Bahan (Alas + Selimut):
$$L_{alas} = \frac{32 \times 24}{2} = 384 \text{ cm}^2$$ $$L_{selimut} = 80 \times 30 = 2400 \text{ cm}^2$$ $$L_{total} = 384 + 2400 = 2.784 \text{ cm}^2$$4. Luas Permukaan Balok
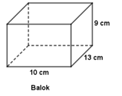
Hitunglah luas permukaan dari balok berikut (Panjang 10 cm, Lebar 13 cm, Tinggi 9 cm)..
Penyelesaian:
$$LP = 2(pl + pt + lt)$$ $$LP = 2((10 \cdot 13) + (10 \cdot 9) + (13 \cdot 9))$$ $$LP = 2(130 + 90 + 117)$$ $$LP = 2(337) = 674 \text{ cm}^2$$5. Luas Permukaan Kerucut
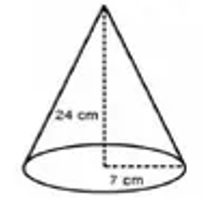
Luas permukaan bangun kerucut di bawah ini adalah... (Jari-jari 7 cm, Tinggi 24 cm)
Penyelesaian:
Cari garis pelukis (\(s\)) dengan teorema Pythagoras:
$$s = \sqrt{7^2 + 24^2} = \sqrt{625} = 25 \text{ cm}$$Hitung Luas Permukaan:
$$LP = \pi r(r + s)$$ $$LP = \frac{22}{7} \cdot 7 (7 + 25)$$ $$LP = 22 \cdot 32 = 704 \text{ cm}^2$$B. Kategori Middle/High (HOTS)—5 Soal
1. Biaya Kaca Akuarium (Tanpa Tutup)
Sebuah akuarium kaca berbentuk balok tanpa tutup memiliki ukuran: Panjang \(100 \text{ cm}\), Lebar \(50 \text{ cm}\), dan Tinggi \(80 \text{ cm}\). Jika harga kaca per \(m^2\) adalah Rp150.000,00, berapakah biaya total pembelian kaca?
Penyelesaian:
Luas Permukaan (LP) Tanpa Tutup:
$$LP = (P \times L) + 2(P \times T) + 2(L \times T)$$ $$LP = (100 \times 50) + 2(100 \times 80) + 2(50 \times 80)$$ $$LP = 5000 + 16000 + 8000 = 29.000 \text{ cm}^2 = 2,9 \text{ m}^2$$Total Biaya:
$$Biaya = 2,9 \times \text{Rp}150.000,00 = \text{Rp}435.000,00$$2. Perbandingan Volume Tabung Sebangun
Sebuah pabrik memproduksi dua jenis kaleng minuman sebangun. Kaleng besar tinggi \(12 \text{ cm}\) dan volume \(300 \text{ ml}\). Jika kaleng kecil tinggi \(6 \text{ cm}\), berapakah volume kaleng kecil tersebut?
Penyelesaian:
Faktor skala Panjang:
$$k = \frac{T_{kecil}}{T_{besar}} = \frac{6}{12} = 0,5$$Perbandingan Volume:
$$\frac{V_{kecil}}{V_{besar}} = k^3 = \left(\frac{1}{2}\right)^3 = \frac{1}{8}$$ $$V_{kecil} = \frac{1}{8} \times 300 \text{ ml} = 37,5 \text{ ml}$$3. Luas Permukaan Gabungan (Kerucut & Tabung)
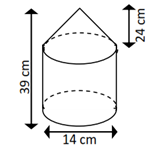
Luas permukaan bangun gabungan di atas adalah... (Diameter 14 cm, Tinggi total 39 cm, Tinggi kerucut 24 cm)
Penyelesaian:
Diketahui \(d=14 \rightarrow r=7\). Tinggi kerucut \(t_k=24\). Tinggi tabung \(t_t = 39 - 24 = 15 \text{ cm}\).
Cari garis pelukis kerucut (\(s\)): \(\sqrt{7^2 + 24^2} = 25 \text{ cm}\).
1. LP Kerucut tanpa alas (\(\pi rs\)):
$$= \frac{22}{7} \times 7 \times 25 = 550 \text{ cm}^2$$2. LP Tabung tanpa tutup (\(\pi r(r + 2t)\)):
$$= \frac{22}{7} \times 7 (7 + 2 \times 15) = 22(37) = 814 \text{ cm}^2$$Total LP:
$$550 + 814 = 1.364 \text{ cm}^2$$4. Sudut Luar Segitiga
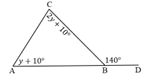
Berapakah nilai \(y\) pada gambar di atas? (Sudut luar \(140^\circ\))
Penyelesaian:
Sudut luar sama dengan jumlah dua sudut dalam yang tidak berpelurus dengannya:
$$140 = (2y + 10) + (y + 10)$$ $$140 = 3y + 20$$ $$120 = 3y$$ $$y = 40$$5. Pasangan Sudut Berpelurus
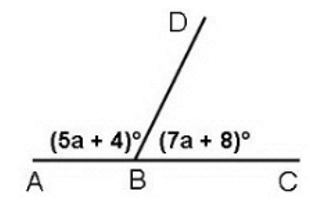
Besar sudut CBD pada gambar di atas adalah....
Penyelesaian:
Jumlah sudut berpelurus adalah \(180^\circ\):
$$(5a + 4) + (7a + 8) = 180$$ $$12a + 12 = 180$$ $$12a = 168 \rightarrow a = 14$$Maka besar sudut CBD (\(7a+8\)):
$$\angle CBD = 7(14) + 8 = 98 + 8 = 106^\circ$$C. Mini TKA—5 Soal
1. Sudut pada Segitiga Sejajar
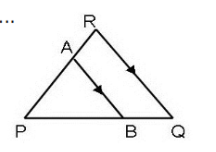
Jika \(\angle RPQ = 70^\circ\) dan \(\angle PQR = 50^\circ\), maka besar sudut RAB adalah... (Garis AB sejajar dengan PQ)
Penyelesaian:
Karena garis AB sejajar dengan PQ, maka sudut \(\angle RAB\) dan sudut \(\angle RPQ\) adalah sudut sehadap.
Sehingga:
$$\angle RAB = \angle RPQ = 70^\circ$$2. Sudut Luar Berseberangan
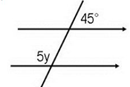
Nilai \(y\) pada gambar garis sejajar di atas adalah....
Penyelesaian:
Sudut \(45^\circ\) dan \(5y\) merupakan pasangan sudut luar berseberangan, sehingga besarnya sama.
$$5y = 45^\circ$$ $$y = 9^\circ$$3. Sudut Pelurus KLN
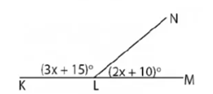
Besar sudut pelurus KLN adalah....
Penyelesaian:
1. Cari nilai \(x\) (Jumlah sudut \(180^\circ\)):
$$(3x + 15) + (2x + 10) = 180$$ $$5x + 25 = 180$$ $$5x = 155 \rightarrow x = 31$$2. Cari besar \(\angle KLN\):
$$\angle KLN = 3(31) + 15 = 93 + 15 = 108^\circ$$3. Sudut pelurus dari KLN adalah pelengkapnya (yaitu \(\angle MLN\)):
$$\text{Pelurus KLN} = 180 - 108 = 72^\circ$$(Catatan: Jika soal menanyakan besar sudut KLN itu sendiri, jawabannya 108. Jika menanyakan pelurusnya, jawabannya 72).
4. Volume Limas (Analisis Tinggi)
Kiki membuat kerajinan dari gypsum berbentuk limas. Alas kerajinan tersebut berbentuk jajargenjang dengan panjang alas \(15 \text{ cm}\), tinggi \(10 \text{ cm}\). Jika volume kerajinan tersebut \(600 \text{ cm}^3\), tinggi kerajinan yang dibuat Kiki adalah....
Penyelesaian:
Luas Alas (Jajargenjang):
$$L_{alas} = a \times t = 15 \times 10 = 150 \text{ cm}^2$$Rumus Volume Limas:
$$V = \frac{1}{3} \times L_{alas} \times t_{limas}$$ $$600 = \frac{1}{3} \times 150 \times t_{limas}$$ $$600 = 50 \times t_{limas}$$ $$t_{limas} = \frac{600}{50} = 12 \text{ cm}$$5. Luas Permukaan Bola (Analisis Biaya)
Sebuah pabrik akan memproduksi 250 buah bola pingpong berdiameter \(6 \text{ cm}\). Jika biaya produksi total adalah Rp42.390.000,00, berapakah harga bahan bola pingpong tersebut per \(\text{cm}^2\)?
Penyelesaian:
Luas Permukaan 1 Bola (\(\pi = 3,14\)):
$$LP = \pi d^2 = 3,14 \times 6 \times 6 = 113,04 \text{ cm}^2$$Total Luas untuk 250 Bola:
$$L_{total} = 250 \times 113,04 = 28.260 \text{ cm}^2$$Harga per \(\text{cm}^2\):
$$\text{Harga} = \frac{\text{Biaya Total}}{\text{Luas Total}} = \frac{42.390.000}{28.260} = \text{Rp}1.500,00$$